| Tableaux, is a small application that helps you constructing a tableaus to process predicate logical information, such as checking the validity of a given inference or the consistency of a given set of formulas. |
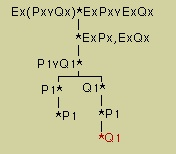
|
Week 8
| Tableaux, is a small application that helps you constructing a tableaus to process predicate logical information, such as checking the validity of a given inference or the consistency of a given set of formulas. |
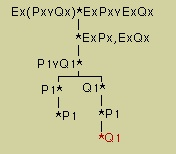
|
Week 7

|
The verificator is a small application for evaluation of predicate logical formulas. You can construct a model (situation) and then evaluate formulas on this model. By making use of free variables in formulas it is also possible to retrieve information about the object within the model. |
Week 2
| The first is an update-calculator with which you can perform updates and tests by means of propositional formulas. It checks the validity of an inference. The premises (assumptions) of the inference enforce eliminative updates, and a formula that is tested after that is valid if all the situations which are left over make the tested formula true. |

|
| The second, called the truth-tabulator computes a complete truth-table for a given formula step-by-step. You can use it to test your own pen-and-paper work. |
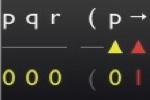
|
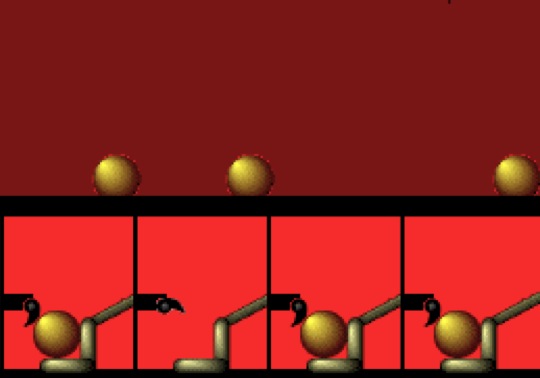
Week 1 Two animations from the text of the first introductory chapter:
|
The first binary addition mechanism as described by Leibniz (around 1705) as described in hand written manuscript `Mechanica Dyadica'. Leibniz developed different decimal calculators, but when he invented his binary calculus, he realized that this system is much easier to use for mechanization of school arithmetics (Leibniz wasn't the first who came up with binary arithmetic, but he certainly was the first who studied and explained it in a systematic way. If you read French, learn it from Leibniz himself.) |
|
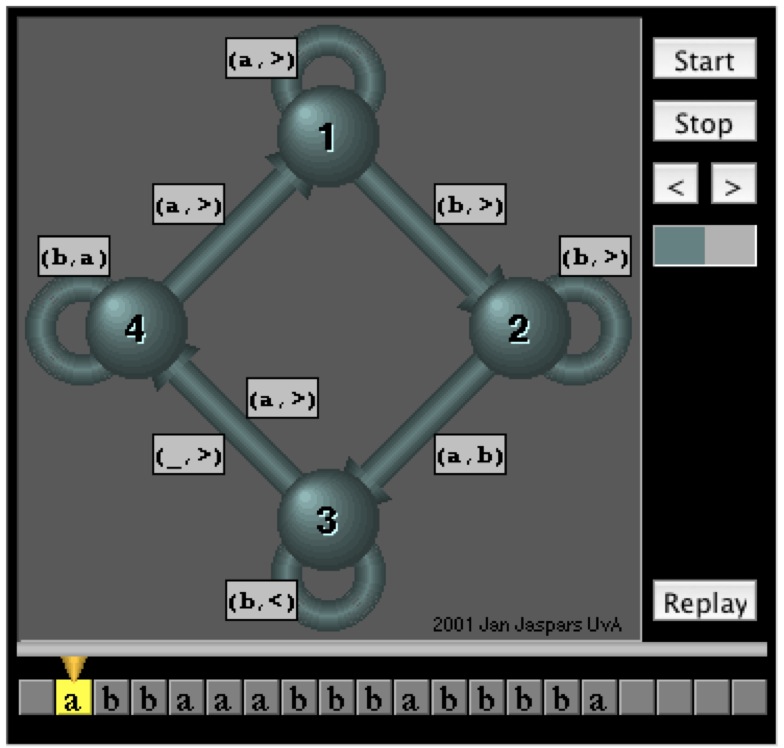
A simple example of a Turingmachine . Let it run and try to figure out what this machine does. After some time it won't take so much effort to understand how the algorithm works. Alan Turing, a British logicican, claimed (1935) that for each problem that can be solved by mechanic means a Turingmachine exists which solves it. This gave a precise and easy to use mathematical definition of computability. Imagine, this was all done before computers existed, and Turing's definition still stands. In the late fourties and early fifties of the previous century Turing worked on the development of computers for which he made use of his earlier theoretical ideas. |